Glosario Geología / Término
Índices cristalográficos (notaciones cristalograficas)
Sistema de notación de formas y caras cristalográficas basado en las razones de intersección. Tomando estas razones de la forma unidad seleccionada (Parámetros), y utilizándolas para reducir las proporciones de intersección de las otras formas a valores integrales, resultan unos índices que son conocidos como índices de Weiss. En este sistema, las caras paralelas a un eje tienen un índice de valor infinito; p. ej., 1 α 2 implica que la cara es paralela al eje b. Esto trae consigo serias complicaciones cuando tiene que utilizarse este tipo de notación y, consecuentemente, hoy día han sido reemplazados los índices de Weiss por los índices de Miller. Estos derivan de los índices de Weiss, estableciendo las fracciones inversas y reduciendo a números enteros; e.g. de los ejemplos de arriba:
1. La notación de Weiss 1 α 2 se convierte en 1 0 ½, y multiplicado por 2, se obtiene la notación de Miller 2 0 1 (leído «dos – cero - uno» ) (ver ejemplo descrito abajo).
Las letras h, k, l se utilizan como símbolos generales para representar los índices (h, j, k, l en el sistema hexagonal).
Los índices de las caras que cortan los extremos de los ejes negativos se indican por medio de una raya sobre el número apropiado; p. ej., 2 0 1 es la cara negativa correspondiente a nuestro ejemplo anterior. Si un índice se representa entre llaves, {h, k,l} , indica que es el índice de una forma, y debe interpretarse como la cara h k l junto con todas las otras caras de la forma requerida por la clase de simetría involucrada. El símbolo [h k I] entre corchetes es un símbolo zonal, estrictamente un sistema de coordenadas.
En el sistema hexagonal la suma algebráica de h, j y k es necesariamente cero.
Ejemplo práctico de la derivación de los índices cristalográficos. A partir de los ángulos interfaciales de las caras, medidos por un goniómetro, es posible calcular las razones de intersección:
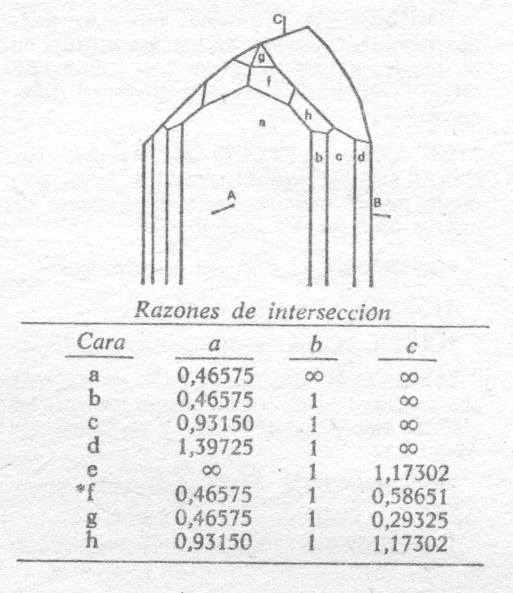
La cara marcada con asterisco se elige como forma unidad y sus razones de intersección se utilizan como parámetros. Dividiendo las razones de intersección para las caras por los parámetros, obtenemos los índices de Weiss.
Índices de Weiss | |||
Cara | a | b | c |
a | 1 | 2. α | 3. α |
b | 1 | 1 | 4. α |
c | 2 | 1 | 5. α |
d | 3 | 1 | 6. α |
e | 7. α | 1 | 2 |
f | 1 | 1 | 1 |
g | 1 | 1 | ½ |
h | 2 | 1 | 2 |
Los inversos de los índices de Weiss dan lugar a los índices de Miller, pasando las fracciones a números enteros si es necesario:
Índices de Miller | |||
Cara | a | b | c |
a | 1 | 0 | 0 |
b | 1 | 1 | 0 |
c | 1 | 2 | 0 |
d | 1 | 3 | 0 |
e | 0 | 2 | 1 |
f | 1 | 1 | 1 |
g | 1 | 1 | 2 |
h | 1 | 2 | 1 |
Enlace permanente: Índices cristalográficos (notaciones cristalograficas) - Fecha de creación: 2012-04-08