Coeficiente de asimetría de Pearson

El coeficiente de asimetría de Pearson es un estadistico que mide la desviación de la simetría, expresada la diferencia entre la media y la mediana con respecto a la desviación estándar del grupo de mediciones.

Es pues un un valor que indica la asimetría de la distribución estadística. Simbólicamente se representa por A_s, y se obtiene mediante la siguiente fórmula:

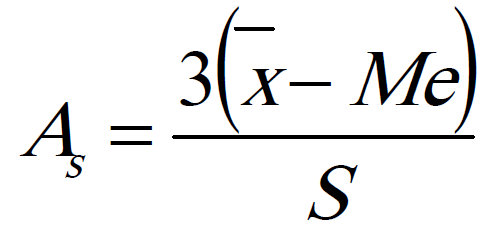
Donde:

X es la media aritmética.

S es la desviación estándar.

Me es la mediana.

Mide el grado de asimetría de la distribución con respecto a la media. Un valor positivo de este indicador significa que la distribución se encuentra sesgada hacia la izquierda (orientación positiva). Un resultado negativo significa que la distribución se sesga a la derecha.

Así pues, si:

A_s = 0 Entonces la distribución es simétrica.

A_s > 0 Entonces la distribución es asimétrica hacia la derecha o tiene sesgo positivo.

A_s < 0 Entonces la distribución es asimétrica hacia la izquierda o tiene sesgo negativo.

Sólo se puede utilizar en distribuciones uniformes, unimodales y moderadamente asimétricas.

Índice de asimetría de Pearson

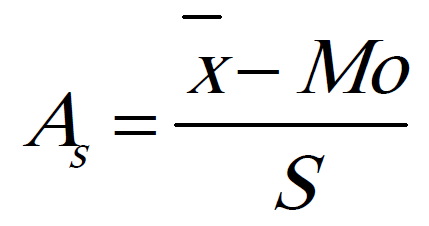
Donde:

x es la media aritmética.

Mo es la moda.

S es la desviación estándar.

Se basa en que en distribuciones simétricas la media de la distribución es igual a la moda.

A_p = (μ - moda) / σ ,

donde es el momento ordinario de orden 1, que corresponde a la media aritmética de la variable .

Si la distribución es simétrica, μ = moda y A_p = 0.

Si la distribución es asimétrica positiva la media se sitúa por encima de la moda y, por tanto, A_p > 0.

Sólo se puede utilizar en distribuciones uniformes, unimodales y moderadamente asimétricas.

Interpretación del índice de asimetría de Pearson:

• Si A_p < 0: la distribución tiene una asimetría negativa, puesto que la media es menor que la moda.
• Si A_p = 0: la distribución es simétrica.
• Si A_p > 0: la distribución tiene una asimetría positiva, ya que la media es mayor que la moda.