Coeficiente de correlación lineal de Pearson

Es un número que mide la intensidad de la asociación lineal entre dos variables.

El coeficiente de correlación se representa simbólicamente por "r".

Este coeficiente se aplica cuando la relación que puede existir entre las variables es lineal (es decir, si representáramos en un gráfico los pares de valores de las dos variables, la nube de puntos se aproximaría a una recta).

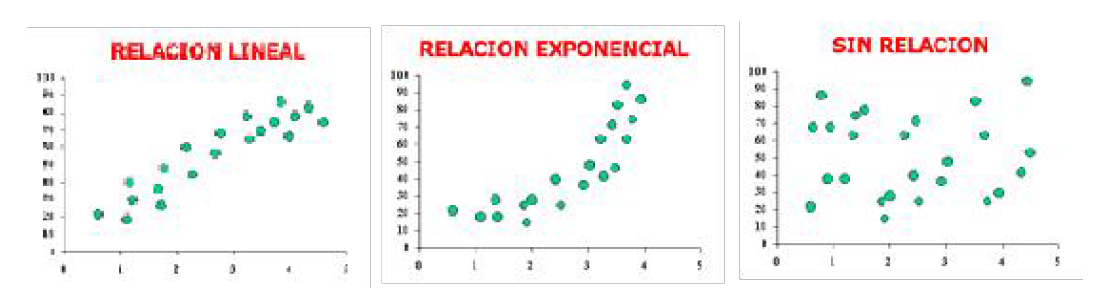
No obstante, puede que exista una relación que no sea lineal, sino exponencial, parabólica, etc. En estos casos, el coeficiente de correlación lineal mediría mal la intensidad de la relación de las variables, por lo que convendría utilizar un tipo de coeficiente más apropiado.

El coeficiente de correlación lineal se calcula aplicando la siguiente fórmula:

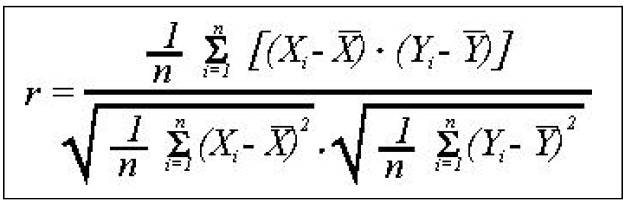
O su equivalente:

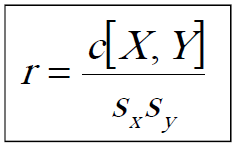
Los valores que puede tomar el coeficiente de correlación "r" son:

-1 ≤ r ≤ 1

Si "r" > 0 La correlación lineal es positiva (si sube el valor de una variable sube el de la otra). La correlación es tanto más fuerte cuanto más se aproxime a 1.

Si "r" < 0 La correlación lineal es negativa (si sube el valor de una variable disminuye el de la otra). La correlación negativa es tanto más fuerte cuanto más se aproxime a -1.

Si "r" = 0 No existe correlación lineal entre las variables, aunque podría existir otro tipo de correlación (parabólica, exponencial, etc.)

De todos modos, aunque el valor de "r" fuera próximo a 1 ó -1, tampoco esto quiere decir obligatoriamente que existe una relación de causa-efecto entre las dos variables, ya que este resultado podría haberse debido al puro azar.