Glosario Termodinámica / Término

Proceso Politrópico

Un proceso de expansión y compresión de gases donde la presión y el volumen se relacionen, como sucede a menudo, mediante una ecuación de la forma:

PVn = C

Donde n y C son constantes, se denomina proceso politrópico. Así pues, en un proceso de esta clase, el producto de la presión y la enésima potencia del volumen es una constante. Dicho de otro modo: si P1 y V1 son la presión y el volumen en un estado del proceso, y P2 y V2 son la presión y el volumen en otro estado del proceso, entonces:

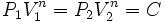
En un proceso politrópico tenemos pues que, al despejar, la presión viene dada por:

P = CV − n

Puesto que el trabajo de frontera realizado desde el comienzo de la expansión o compresión hasta el estado final viene dado por:

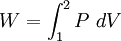
$W=\int_1^2P\ dV$

Tenemos que el trabajo producido en un proceso politrópico se calcula mediante:

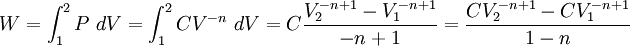
$W=\int_1^2P\ dV=\int_1^2CV^{-n}\ dV=C\frac{V_2^{-n+1}-V_1^{-n+1}}{-n+1}=\frac{CV_2^{-n+1}-CV_1^{-n+1}}{1-n}$

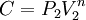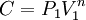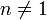En el numerador, podemos tomar C=P_2V_2^n en el primer término y C=P_1V_1^n en el segundo término y así obtener una formula sencilla que permite obtener el trabajo realizado en un proceso politrópico para $n\neq 1$ :

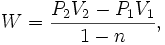
$W=\frac{P_2V_2-P_1V_1}{1-n},$

Si n = 1, entonces:

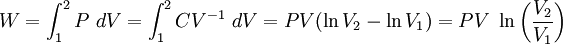
$W=\int_1^2 P\ dV=\int_1^2CV^{-1}\ dV=PV(\ln V_2-\ln V_1)=PV\ \ln\left(\frac{V_2}{V_1}\right)$

Para el caso de un gas ideal, donde PV = nRT, la fórmula del trabajo en un proceso politrópico se convierte en:

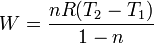
$W=\frac{nR(T_2-T_1)}{1-n}$

Enlace permanente: Proceso Politrópico - Fecha de actualización: 2018-08-31 - Fecha de creación: 2018-08-31

< Proceso Isotérmico Glosario Termodinámica Propiedades Extensivas >

Proceso Politrópico

Novedades

Actualizaciones

Glosarios especializados